Iterative Methods
Why do we need another method to solve a set of simultaneous linear equations?
In certain cases, such as when a system of equations is large, iterative methods of solving equations are more advantageous. Elimination methods, such as Gaussian elimination, are prone to large round-off errors for a large set of equations. Iterative methods, give the user control of the round-off error. Also, if the physics of the problem are well known, initial guesses needed in iterative methods can be made more judiciously leading to faster convergence.
Jacobi's Method
The Jacobi method is a method of solving a matrix equation on a matrix that has no zeros along its main diagonal. Each diagonal element is solved for, and an approximate value plugged in. The process is then iterated until it converges.
The Jacobi method is easily derived by examining each of the n equations in the linear system of equations Ax = b in isolation. If, in the i-th equation:
Solve for the value of Xi while assuming the other entries of x remain fixed. This suggests an iterative method:
In this method, the order in which the equations are examined is irrelevant, since the Jacobi method treats them independently. The definition of the Jacobi method can be expressed with matrices as:
References:
http://mathworld.wolfram.com/JacobiMethod.html
http://www.nhcue.edu.tw/~jinnliu/teaching/nde07/Lecture3.pdf
Gauss-Seidel Method
The Gauss-Seidel method is a technique used to solve a linear system of equations.
The method is similar to the Jacobi method and in the same way strict or irreducible diagonal dominance of the system is sufficient to ensure convergence, meaning the method will work.
Procedure:
If the diagonal elements are non-zero
The equations can be rewritten in summaration form as:
Now to find Xi’s, one assumes an initial guess for the Xi’s and then uses the rewritten equations to calculate the new estimates. Remember, one always uses the most recent estimates to calculate the next estimates, Xi. At the end of each iteration, one calculates the absolute relative approximate error for each Xi.
Important: Remember to use the most recent value of xi. Which means to apply values calculated to the calculations remaining in the current iteration.
Example:
Refrences:
http://numericalmethods.eng.usf.edu/topics/gauss_seidel.html
http://www.cfd-online.com/Wiki/Gauss-Seidel_method
Successive Overrelaxation Method (SOR)
The successive overrelaxation method (SOR) is a method of solving a linear system of equations ![]() derived by extrapolating the Gauss-Seidel method. This extrapolation takes the form of a weighted average between the previous iterate and the computed Gauss-Seidel iterate successively for each component,
derived by extrapolating the Gauss-Seidel method. This extrapolation takes the form of a weighted average between the previous iterate and the computed Gauss-Seidel iterate successively for each component,
where ![]() denotes a Gauss-Seidel iterate and
denotes a Gauss-Seidel iterate and ![]() is the extrapolation factor. The idea is to choose a value for
is the extrapolation factor. The idea is to choose a value for ![]() that will accelerate the rate of convergence of the iterates to the solution.
that will accelerate the rate of convergence of the iterates to the solution.
In matrix terms, the SOR algorithm can be written as





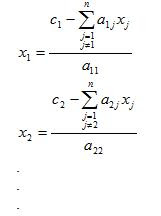











Publicar un comentario